在医院推行质量持续改进计划时，七大品管手法是我们经常采用的工具，它们直接影响改进措施的成效。本文将重点介绍其中一种手法——直方图。

它能够精确地分析数据分布，帮助我们识别数据的集中趋势、离散程度以及是否存在异常值。通过直方图，我们可以直观地看到数据的分布形态，从而为后续的数据分析和决策提供有力支持。

一、什么是直方图

1.直方图又称质量分布图，是对定量数据分布情况的一种图形，由一系列的矩形（直方柱）所组成，表示资料变化情况的一种工具。

2.将所搜集的数据、特性值或结果值、在一定范围的横轴上加以区分成几个相等的区间，依其分布的次数，以柱形表示。

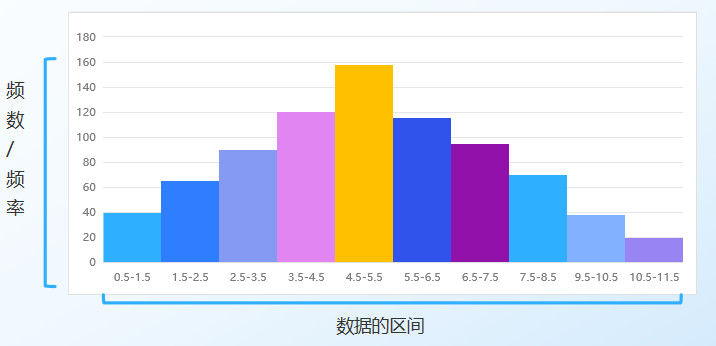
二、直方图用途

在许多医学研究中所搜集到的数据，通常是庞大与杂乱的，在直观上并无法立马观察出其趋势与分布，在处理许多数据时，可先将资料进行分组，让数据更具系统与条理。针对连续型的资料更可从中观察并研究这批数据的范围、集中、分散等分布情况。

三、直方图绘制步骤

1.由全体数据中找到最大值与最小值。

2.计算全距。（连续数据中最大值与最小值的差）

3.确定组数。

组数就是直方图柱形数量，组数的计算是根据数据数量的多少来决定。组数过少，固然可得到相当简单的表格，但失去了次数分配的本质与意义；组数过多，虽然表格详尽，但无法达到简化的目的。通常，应先将异常值剔除后再行分组。

Ø 可用数学家史特吉斯（Sturgcs）提出的公式，根据测定次数n来计算组数K。

公式：（K）=1 + 3.321gn 例：n=60，则k=1+3.32lg60=1+3.32 ×1.78 = 6.9，即约可分为6组或7组。

Ø 经验法：一般为8～12组为宜。

4.确定组距。

组距=全距/组数（K）

5.确定各组的上组界与下组界。

Ø 最小一组的下组界=全部数据的最小值——测量值最小位数/2（测量值最小位数：整数位的测量值最小位数为1，小数点1位的测量值最小位数为0.1，）

Ø 最小一组的上组界=最小一组的下组界+组距，依此类推。

6.作次数分配表。

统计出位于各组界间之数据个数。

7.制作直方图。

用X轴表示数值，Y轴表示次数，绘出直方图。

四、直方图异常分析

当直方图出现异常分布时，可能意味着数据存在异常或疾病状态。常见的异常分布包括：

Ø 偏态分布：数据分布向一侧偏移，可能表示患者存在某种异常状态。

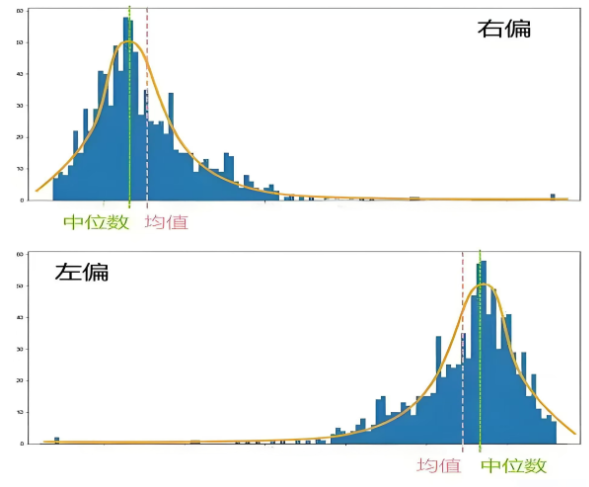
Ø 双峰分布：数据分布存在两个明显的峰值，可能表示患者存在两种不同的健康状态或疾病类型。

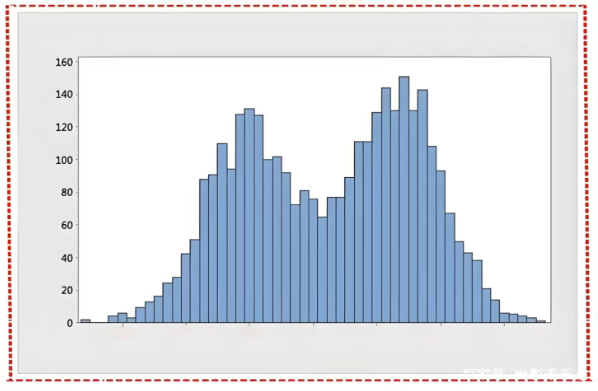
Ø 异常值：直方图尾部出现极少数极高或极低的数值，可能表示存在测量误差或患者存在特殊疾病状态。

五、直方图使用的注意事项

1.异常值应去除后再分组。

2.对于从样本测定值推测群体形态，直方图是最简单有效的方法。

3.应取得详细的数据资料（例如时间、测定者、环境条件等）。

4.进行工作过程管理及分析改善时，用层别法将更容易找出问题的症结点，对于品质的改善有事半功倍的效果。

作者

杨萍

主管护师

医院质量管理办公室干事